Our group is concerned with research in quantum-information and computing and the intersection between these fields. There are research positions (Master's and Bachelor's theses) and internships if you are interested. For all inquiries concerning research positions and internships, please contact me:

zraissi[at]mail.uni-paderborn[dot]de

z.raissi2[at]gmail[dot]com

Overview:

Quantum mechanics is already 100 years old, during this time it was discovered that quantum physics has the potential to revolutionize information security, enabling quantum computers, and solving a number of outstanding problems in physics, computer science, chemistry, and biomedicine. The overarching goal of our group is to study and understand how to exploit quantum mechanics to develop new technologies that are otherwise impossible. The main interests the Quantum Information group at Paderborn University is concerned with are research on:

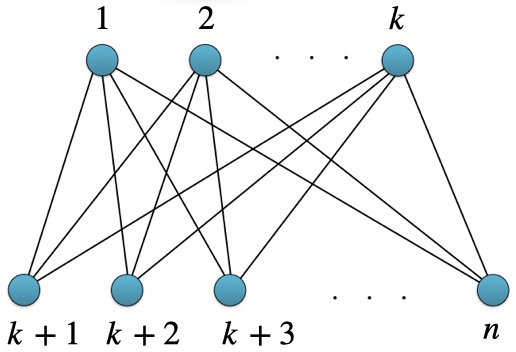* ) Many-body Entanglement; Quantum entanglement is the physical phenomenon that occurs when a group of particles are generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the group cannot be described independently of the state of the others. Entanglement is a primary feature of quantum mechanics not present in classical mechanics. Having access to an entangled state enables quantum information-processing tasks that cannot be achieved classically, such as teleportation, measurement-based quantum computation, and entanglement-based quantum communication. Despite its importance, we are still far from a complete understanding of entanglement. Therefore, we have some questions in mind we would like to work on:

- How to measure / characterize / quantify entanglement of many-body quantum systems?

- What are the most useful states for a given quantum application?

- Finding connection between multipartite entanglement and classical and quantum error correcting codes.

- As entanglement cannot be created or enhanced using local operation and having classical communications, how one can classify the entangled states based on this fact?

- How can we generalise the EPR or Bell state to an arbitrary number of parties?

* ) Quantum Error Correction; Similar to classical error correction, which plays a central role in classical information theory, quantum error correction is similarly foundational in quantum information theory. Both are concerned with the fundamental problem of communication, as well as information storage, in the presence of noise. However, there are primary differences between classical and quantum error correcting codes, namely:

1. a quantum state can be in a superposition of multiple different classical states

2. any measurement of the superposition might collapse the quantum state into one of its classical components

3. copying quantum information is not possible due to the no-cloning theorem

We should note that error correction is especially important in quantum computers because efficient quantum algorithms are possible if we can stop imprecision. There are interesting open questions in this area as well:

- Is there any connection between classical and quantum error correcting codes?

- Can we use existing quantum error correcting codes to construct new ones?

- Can we use holographic models to construct quantum error correcting codes?

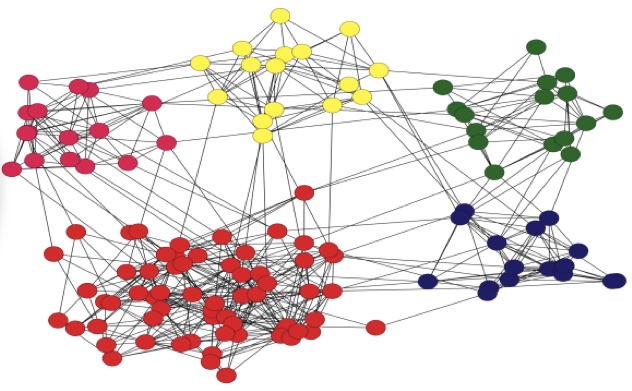* ) Quantum Networks; are like the classical networks we use in everyday life to transmit and share digital information. However, quantum networks use uniquely quantum phenomena, like superposition, no-cloning, and entanglement, that are not available to classical networks. There are different ways of defining the entanglement between neighboring qubits. So far, we have only used the method in which one link between neighboring nodes is given by one pair of entangled qubits, for example, atoms. In other words, one link in a quantum network represents the entanglement between two qubits. As quantum networks are an important element of quantum computing and quantum communication systems, increasing our knowledge while studying multipartite entangled states is very important. Therefore, we can think of the following interesting questions in this area:

-What other methods of generating arbitrary quantum networks can we consider?

-How does measuring a single qubit changes the structure/model of a network?

-How to characterize the graphs by their robustness against losses and local noise?

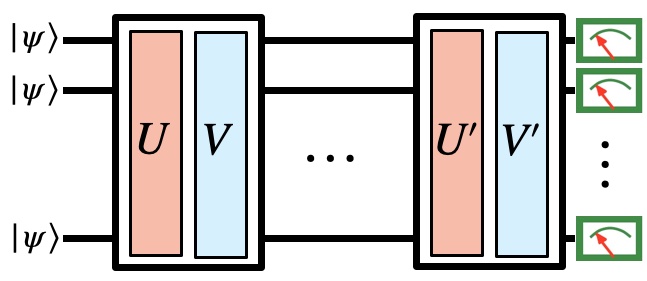* ) Quantum Algorithms; A quantum computer exploits quantum mechanical phenomena to operate, which cannot be done by any machine based only on the laws of classical physics. In mathematics and computer science, an algorithm is a finite sequence of instructions or a step-by-step procedure for solving a problem. The term quantum algorithm is usually used for algorithms that seem inherently quantum or use some essential feature of quantum computation, such as quantum superposition or entanglement. In principle, running all classical algorithms on a quantum computer is possible, however, the advantage that quantum algorithms have is running on a quantum computer and achieving a speedup, or other efficiency improvement, over any possible classical algorithm. In this area of science, one can think of some interesting projects and ideas that we can discuss more if you are interested.